Senin, 28 Februari 2011
Minggu, 27 Februari 2011
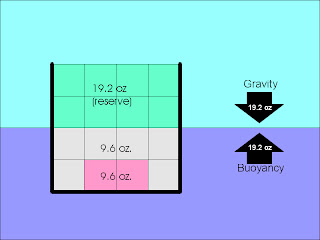
RESERVE BUOYANCY
sample 1:
A box shaped vessel 105m x 30m x 20m is floating upright in fresh water. if the displacement is 19500 tonnes, find the volume of reserve buoyancy.
Volume of water displaced = Mass/Density = 19500/1.000 = 19500 m3
Volume of vessel = 105 x 30 x 20 = 63000 m3
Reserve buoyancy = Volume of vessel - volume of water displaced
= 63000 m3 - 19500 m3 = 43500 m3
DENSITY AND SPECIFIC GRAVITY
Density is define as "mass per unit volume".
FW = 1000 kg per m3 or 1.000 ton/m3
SW = 1025 kg per m3 or 1.025 ton/m3
Density in kg/m3 = 1000 x SG
sample 1:
When double bottom tank is full of fresh water it holds 120 tonnes. Find how many tonnes of oil of relative density 0.84 it will hold.
Relative density = Mass of Oil / Mass of FW
Mass of Oil = Mass of FW x relative density
= 120 x 0.84 tonnes
= 100.8 tonnes of oil
sample 2:
A tank measures 20m x 24m x 10.5m and contains oil of relative density 0.84. Find the mass of oil it contains when the ullage is 2.5m. Ullage is the distance from the liquid surface in the tank to the top of the tank.
Volume of oil = L x B x D
= 20 x 24 x 8
Density of oil = SG x 1000
= 840 kg/m3 or 0.84 t/m3
Mass of oil = Volume x density
= 20 x 24 x 8 x 0.84
= 3225.6 tonnes
Specific Gravity of some liquids
Salt water = 1.025 Oil fuel = 0.950 Lubricating fuel = 0.900
Fresh water = 1.000 Diesel fuel = 0.900
FW = 1000 kg per m3 or 1.000 ton/m3
SW = 1025 kg per m3 or 1.025 ton/m3
Density in kg/m3 = 1000 x SG
sample 1:
When double bottom tank is full of fresh water it holds 120 tonnes. Find how many tonnes of oil of relative density 0.84 it will hold.
Relative density = Mass of Oil / Mass of FW
Mass of Oil = Mass of FW x relative density
= 120 x 0.84 tonnes
= 100.8 tonnes of oil
sample 2:
A tank measures 20m x 24m x 10.5m and contains oil of relative density 0.84. Find the mass of oil it contains when the ullage is 2.5m. Ullage is the distance from the liquid surface in the tank to the top of the tank.
Volume of oil = L x B x D
= 20 x 24 x 8
Density of oil = SG x 1000
= 840 kg/m3 or 0.84 t/m3
Mass of oil = Volume x density
= 20 x 24 x 8 x 0.84
= 3225.6 tonnes
Specific Gravity of some liquids
Salt water = 1.025 Oil fuel = 0.950 Lubricating fuel = 0.900
Fresh water = 1.000 Diesel fuel = 0.900
the mass of each above is 1 ton with various volumes
Jumat, 25 Februari 2011
Effect of change of density when the displacement is constant
When a ship moves from water of one density to water of another density, without there being a change in her mass, the draft will change.
Mass = Volume x Density
The effect on box-shaped vessels
New Volume = Old density or New draft = Old density
Old Volume New density Old draft New density
sample 1:
A box-shaped vessel floats at mean draft of 2.1 metres, in dock water of density 1020 kg/m3. Find the mean draft for tha same mass displacement in salt water of density 1025 kg/m3.
answer: New draft = 2.09 metres (you can try the above formula)
sample 2:
A box-shaped vessel float upright on an even keel as shown in fresh water of density 1000 kg/m3 and the CoB is 0.50 m above the keel. Find the height of the CoB above the keel when the vessel is floating in salt water of density 1025 kg/m3.
CoB of Box shaped vessel : KB = 0.5 draft
Answer:
In fresh water: KB=0.5m and since KB = 0.5draft, then draft = 1 m
In salt water : New draft = Old draft x (Old density / New density)
= 1 x 1000/1025
= 0.976 m
New KB = 0.5 new draft
= 0.488 ~0.49 m
The effect on box-shaped vessels
Mass = Volume x Density
The effect on box-shaped vessels
New Volume = Old density or New draft = Old density
Old Volume New density Old draft New density
sample 1:
A box-shaped vessel floats at mean draft of 2.1 metres, in dock water of density 1020 kg/m3. Find the mean draft for tha same mass displacement in salt water of density 1025 kg/m3.
answer: New draft = 2.09 metres (you can try the above formula)
sample 2:
A box-shaped vessel float upright on an even keel as shown in fresh water of density 1000 kg/m3 and the CoB is 0.50 m above the keel. Find the height of the CoB above the keel when the vessel is floating in salt water of density 1025 kg/m3.
CoB of Box shaped vessel : KB = 0.5 draft
Answer:
In fresh water: KB=0.5m and since KB = 0.5draft, then draft = 1 m
In salt water : New draft = Old draft x (Old density / New density)
= 1 x 1000/1025
= 0.976 m
New KB = 0.5 new draft
= 0.488 ~0.49 m
The effect on box-shaped vessels
New displacement = Old Displacement
New volume x New density = Old volume x Old density
New volume = Old density
Old volume New density
FWA (Fresh Water Allowance) = number of millimeters by which the mean draft changes when a ship passes from salt water to fresh water or vice versa, whilst floating at the loaded draft.
FWA (in mm) = Displacement (W in tonnes) / (4 x TPC)
Dock Water Allowance = FWA (1025 - density of Dock Water) /25
sample 3:A ship is loading in dock water of density 1010 kg/m3 FWA=150 mm. Find the change in draft on entering salt water.
answer:
Let x = the change in draft in mm, then:
x / FWA = (1025 - 1010) / 25
x = 150 x (15/25)
x = 90 mm
Draft will decrease by 90 mm, i.e. 9 cm
Langganan:
Komentar (Atom)